1. 문제 설명
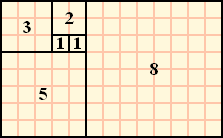
대구 달성공원에 놀러 온 지수는 최근에 새로 만든 타일 장식물을 보게 되었다. 타일 장식물은 정사각형 타일을 붙여 만든 형태였는데, 한 변이 1인 정사각형 타일부터 시작하여 마치 앵무조개의 나선 모양처럼 점점 큰 타일을 붙인 형태였다. 타일 장식물의 일부를 그리면 다음과 같다.
그림에서 타일에 적힌 수는 각 타일의 한 변의 길이를 나타낸다. 타일 장식물을 구성하는 정사각형 타일 한 변의 길이를 안쪽 타일부터 시작하여 차례로 적으면 다음과 같다.
[1, 1, 2, 3, 5, 8, .]
지수는 문득 이러한 타일들로 구성되는 큰 직사각형의 둘레가 궁금해졌다. 예를 들어, 처음 다섯 개의 타일이 구성하는 직사각형(위에서 빨간색으로 표시한 직사각형)의 둘레는 26이다.
타일의 개수 N이 주어질 때, N개의 타일로 구성된 직사각형의 둘레를 return 하도록 solution 함수를 작성하시오.
2. 제한 사항
- N은 1 이상 80 이하인 자연수이다.
3. 입출력 예
| N | return |
| 5 | 26 |
| 6 | 42 |
4. 나의 풀이
문제를 처음 딱 보고 생각이 든 것은 타일의 숫자가 피보나치 수열의 형태를 띤다는 점이었다.
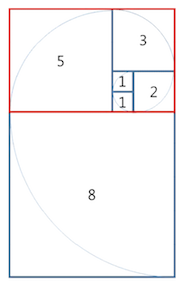
피보나치 수열이란?
첫째 및 둘째 항이 1이며, 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열.
(심지어 위키백과의 그림조차 문제의 그림과 똑같다.)
따라서, 피보나치 함수를 만들고, 각각의 가로 (N-1항 + N-2항)와 세로 (N항 + N-1항) 을 구해 둘레를 구해주면 끝이다.
memo = [0 for i in range(80)]
def fib(n):
if memo[n] > 0:
return memo[n]
if n == 1 or n == 2:
memo[n] = 1
return memo[n]
else:
memo[n] = fib(n - 1) + fib(n - 2)
return memo[n]
def solution(N):
return 2 * (fib(N-2) + 2 * fib(N-1) + fib(N))
이 문제를 풀 당시에는 동적계획법에 대해 자세히 모르는 상태였는데, 문제를 풀고 나서 동적계획법에 대해 공부를 해보니 다행히도 문제의 의도와 일치하게 푼 것 같아 다행이었다. 공부를 하면서 느낀점이 하나 있는데, 학부때 배웠던 피보나치 수열을 구하는 함수는
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
위 코드처럼 재귀함수로 구현하는 방식이었다. 하지만 이렇게 코드를 짜고 나서 제출해보니 시간초과가 떴다. 이유에 대해 알아보니 재귀함수로 n번째 피보나치 수열을 구하면, 재귀 호출로 인해 같은 피보나치 수를 여러번 구해야 해서 시간복잡도가 지수 함수가 돼버린다. 예를 들어,
fib(4)를 구하기 위해서는 재귀로 fib(3) + fib(2)를 구하고, 또 fib(3)과 fib(2)를 구하기 위해서 또 다른 재귀 호출을 하게 되어, 결국 fib(4) = ((fib(1) + fib(0)) + fib(1)) + (fib(1) + fib(0)) 가 되는데, 이 때 같은 함숫값이 여러번 중복되어 계산한다.
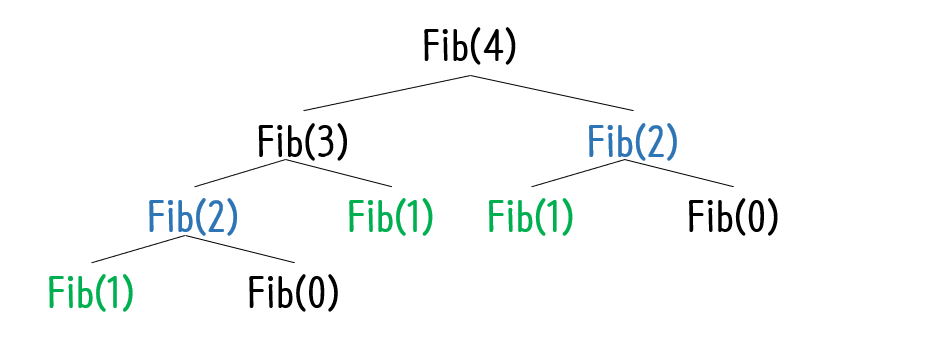
이를 개선하기 위해 메모이제이션을 이용할 수 있다.
메모이제이션(memoization)이란?
컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술. (출처: 위키백과)
말 그대로 필요할 때마다 함수로 값을 구하는 것이 아니라, 메모리에 값을 저장하여 필요할 때마다 꺼내서 쓰는 방법이다. 최대 크기의 리스트를 만들고, 값을 저장한 후 이용할 수 있도록 피보나치 수열 함수를 만들었다.
memo = [0 for i in range(80)]
def fib(n):
if memo[n] > 0: #이전에 저장한 값이 있으면
return memo[n] #가져다 씀
...
else:
memo[n] = fib(n - 1) + fib(n - 2) #없으면 메모리에 저장하고
return memo[n] #반환
중복 계산이 줄어들어 시간 복잡도가 O(n)이 되고, 효율성 테스트를 통과할 수 있었다.
또한, 동적 계획법은 점화식을 이끌어내는 것이 핵심이기 때문에 훈련이 많이 필요하다. 아직 다른 알고리즘이나 자료구조 보다 익숙하지 않아서 더 열심히 해야한다.
문제 링크: https://programmers.co.kr/learn/courses/30/lessons/43104
코딩테스트 연습 - 타일 장식물
대구 달성공원에 놀러 온 지수는 최근에 새로 만든 타일 장식물을 보게 되었다. 타일 장식물은 정사각형 타일을 붙여 만든 형태였는데, 한 변이 1인 정사각형 타일부터 시작하여 마치 앵무조개��
programmers.co.kr
'Problem Solving' 카테고리의 다른 글
| [프로그래머스] 단속카메라 - 그리디(greedy) (python) (0) | 2020.06.14 |
|---|---|
| [프로그래머스] 구명보트 - 그리디(greedy) (python) (0) | 2020.06.13 |
| [프로그래머스] n진수 게임 - ? (python) (0) | 2020.06.09 |
| [프로그래머스] 짝지어 제거하기 - 스택 (python) (0) | 2020.06.09 |
| [프로그래머스] 예산 (level 3) - 이분탐색/이진탐색 (python) (0) | 2020.05.21 |